Finding the Force—Consistent Particle Seeding for Satellite Aerodynamics

Space debris, in an image released by the European Space Agency on 05/06/2013, ID #292643
At AIAA SciTech 2014 —the "largest event for aerospace research, development and technology in the world"—, this paper is part of the AIAA Modeling and Simulation Technologies Conference, in the session "Modeling and Simulation of Space Systems" (MST-07), to be held Jan. 17 (8:00 AM to 12:00 PM). The first author and speaker, J. Brent Parham, was a Barba-group master's student and a Lincoln Scholar at Boston University, graduating in December 2013.
This paper is the product of Brent's MSc thesis research. It presents a ray-tracing Monte Carlo method for estimating the drag coefficient of satellites in low-earth orbit that is is more accurate and more capable than previous methods. Simulating several millions of particles is easy, thanks to parallel computing on multi-core CPUs and GPU accelerators.
Space is full of junk!
In February 2009, an active communications satellite called Iridium 33 crashed into a defunct Russian satellite, Cosmos 2251—a big chunk of space junk—, and died in a giant cloud of space debris. This video shows a software reconstruction of the collision:
Space junk is a big problem for space flight. Just days ago, on 26 Dec. 2013, the US signed a new agreement with Canada to share data on orbiting space debris, and similar agreements are in place with other countries.
To maneuver satellites out of the way of junk, satellite operators need to be able to estimate accurately the orbits and trajectories of satellites. But calculating accelerations due to aerodynamic forces is full of uncertainties.
Aerodynamic drag in space
The force of drag in low-earth orbit is the same as in the lower atmosphere, i.e., the dynamic pressure multiplied by the drag coefficient and area:
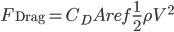
But every term in this equation is more uncertain in space, starting with the neutral density at the edges of the atmosphere. The drag coefficient is a geometry-dependent factor that is hard to obtain for the arbitrarily complicated shapes of satellites. The test-particle Monte Carlo method, introduced in the late 1960s, remains the only way to estimate drag coefficients and include effects like shadowing.
A test-particle Monte Carlo method on GPUs
The test-particle Monte Carlo (TPMC) method traces simulated particles through a control volume containing the spacecraft. Each particle (representing a large collection of actual molecules) then interacts with surfaces to transfer momentum and energy via a surface-interaction model, e.g., diffuse or specular reflection. Thus, the method consists of a Monte-Carlo initialization and a ray tracing algorithm.
To be accurate, a TPMC calculation needs a large number of particles. The computational cost has thus severely limited its application to practical problems in orbital dynamics. Nowadays, we can turn to GPU accelerators for these problems: the algorithm consists of a large collection of independent calculations and is ideal for parallel computing.
Using Nvidia GPUs via the CUDA programming model, we can run larger-scale simulations than have been tried before. At this scale, validating with the analytical solution of drag on a sphere revealed a flaw in the known formulation of ray-tracing MC methods: a simple flaw that no one had seen before, because the simulations were too small. Fixing this flaw required a new particle-seeding scheme, which then led to a nice analytical solution when computing the integral for the correct number flux.
We verified the model with known analytical solutions: a flat plate at an angle of incidence, a convex spherical section and a concave spherical section.
Reference
- "Finding the Force—Consistent Particle Seeding for Satellite Aerodynamics", J. Brent Parham, L. A. Barba. AIAA Modeling and Simulation Technologies Conference organized by American Institute of Aeronautics and Astronautics (January 2014), National Harbor, Maryland.. 10.2514/6.2014-1492 // Preprint arXiv:1312.3691 // Aerospace Research Central
AIAA paper, revised manuscript submitted in December 2013.