Computational Thinking: I do not think it means what you think it means

Credit: Cynthia Solomon/MIT Media Lab
“It’s a basic skill. Right along with the three Rs.” President Obama, on his weekly address just over a month ago, announced the $4-billion Computer Science for All initiative. Reactions quickly spread to make clear that the important skill is not coding, it’s computational thinking. But what does this mean?
As it’s become a buzzword (sadly), let’s have a conversation to clear up the rhetoric and get to deeper meaning. To me, as a computational scientist, the essence is what we can do while interacting with computers, as extensions of our mind, to create and discover. That’s not the popular message today.
The idea of computational thinking was popularized by Jeannette Wing in an article published ten years ago as a Viewpoint in the magazine of the leading society of computer scientists.1 She labels it an “attitude and skill set” that everyone can learn and use. The emphasis is on solving problems by exploiting the fundamental concepts of computer science: abstraction, decomposition, recursion, separation of concerns, and so on. In sum, Wing equates computational thinking with thinking like a computer scientist.
The Wing 2006 Viewpoint has been tremendously influential in the computational-thinking narrative (the paper had 1,841 citations, when checked Mar. 4, 2016 on Google Scholar). But it took us on a detour from the original, powerful idea envisioned by Seymour Papert more than 30 years ago.
On July 2014, I gave a keynote at the SciPy Conference titled “If there is Computational Thinking, there’s Computational Learning,” inviting a leap from the idea of computational thinking to picture how we use computation to create new knowledge, i.e., to learn (in the constructivist sense).
It turns out, the original notion of computational thinking, as envisioned by Seymour Papert, already encompasses the learning I was alluding to. In turn, the popularized meaning of “computational thinking” is a shallower, less powerful idea, as I will explain.
I looked deeper into the matter in a talk at the Berkeley Institute of Data Science, in October 2015. The title was “Computational Thinking and the Pedagogy of Computable Content”—my intention was to expound on why I think Jupyter Notebooks are really a “killer app” in education (as I’d declared at SciPy). By weaving executable code into multi-media content, Jupyter makes seamless the communication between human and machine. Why is this so effective in learning?
As I always tell my students, let’s go back to the source
In 1980, Seymour Papert published the book “Mindstorms: Children, Computers, and Powerful Ideas”2. Papert was co-director, under Marvin Minsky, of the MIT Artificial Intelligence Laboratory from 1967 to 1981. Previously, he had worked with Jean Piaget in Geneva. Piaget was a developmental psychologist best known for pioneering the learning theory known as constructivism: simply put, that learners construct new knowledge (in their minds) from the interaction of their experiences with previous knowledge. Papert, in turn, developed the theory of constructionism, adding the notion that learning is enhanced when the learner is engaged in “constructing a meaningful product.”
In the introduction to Mindstorms, Papert refers to the rise of the personal computer, and how many people imagined it permeating home life and businesses. But he is thinking beyond those roles, to “how computers may affect the way people think and learn.”

Image from the book "Mindstorms"
One striking comment follows a couple of pages later, where the phrase “computer-aided instruction” evokes in Papert the unappealing idea that “the computer is being used to program the child”—his vision, of course, is that the child must program the computer. But this vision is poles apart from the contemporary calls for learning to code. He visualizes this programming as communicating with the computer (having a conversation)—and asserts that “learning to communicate with a computer may change the way other learning takes place.”
“My central focus is not on the machine but on the mind …” —S. Papert
The phrase “computational thinking” appears in Mindstorms (p.182) but without elaboration. We find detailed exposition of the idea in his 1996 paper “An exploration in the space of mathematics educations”3 (whose barely over 150 Google Scholar citations pale to Wing’s viewpoint piece!). Here, Papert explores several dimensions along which we can imagine that mathematics education can be reformed, at the same time as he examines the role of computers in this education.
A few salient ideas in “An exploration … "
To support the rest of my analysis, I picked out four salient ideas from Papert’s 1996 paper:
—The Power Principle: What comes first, ‘using’ or ‘understanding’? The natural mode of learning is to first use, leading slowly to understanding. New ideas are a source of power to do something.
—Project before Problem: “… problems come up in the course of projects and are sometimes ‘solved’ and sometimes ‘dissolved’.”
—Media defines Content: Old-school activities involve making inscriptions on paper, while in Papert’s alternative involve “manipulating a computer-based microworld.” New media open the door to new content.
—Object before Operation: Giving mathematical ideas a “thing-like representation” helps thinking about them.
Throughout, Papert is generous with examples from his experience with children learning with the Logo programming language. He describes students using a Logo object called RANDOM to create color effects on screen, and contrasts it to schools introducing probability using spinners or dice. (“What can children do with this new knowledge besides talk or deal with teacher-initiated problems?”) RANDOM is a mathematical object, and students naturally make new ones, say RANDOM-COLOR, taking in with ease the idea of function, and composition of functions.
Another example deals with the study of the laws of motion, where Papert proposes “dynamics before statics.” Objections to this natural ordering, he says, could raise the arguments that dynamics is conceptually harder than statics, and that it needs calculus. But this “reflects the static nature of pre-computational media.” Calculus may be needed if all that students have is the old medium of pencil and paper: “it is hard because the medium fights the message.” Computing offers multiple new ways of representing motion, making the physics lucid and simple.
“The goal is to use computational thinking to forge ideas.” —SP
Let’s go back now to the contemporary message about computational thinking. Wing refined her meaning in 2010, always focusing on problem-solving and thinking like a computer scientist. She highlights abstraction as the most important process in computational thinking, and adds pattern matching and recursive thinking to the basic toolbox. Google developed their own set of free online resources for educators called “Exploring Computational Thinking” and the BBC offers an online tutorial called “Introduction to Computational Thinking” in their Bitesize section. Both list the key concepts: decomposition, abstraction, pattern recognition, algorithms. Google adds automation, data manipulation and analysis, and simulation. The International Society for Technology in Education (ISTE) and the Computer Science Teachers Association (CSTA) published a set of resources called the "Computational Thinking Toolkit” with videos, slide decks and booklets, and an almost identical message to the previously mentioned.
I do not detract from the value of these efforts—of course they are valuable! The coding initiatives (Hour of Code, etc.) are valuable, too, but Wing and others are quick to declare that computational thinking is not “just programming.”
Well, I say computational thinking does not mean thinking like a computer scientist.

The contemporary message takes an orthogonal direction to Papert, ignoring his Power Principle. It has happened to many powerful ideas when taught in schools (like probability) that they become disempowered: “reduced to shallow manipulation that seldom connects to anything the student experiences as important.”3
Combing through dozens of articles on computational thinking, the emphasis is on problem-solving (low on the problem–project dimension), understanding (low on power), an operational perspective (low on the object–operation dimension), and content priming over media.
It reminds me of the New Math of the 1960s, which fashioned mathematics in a dramatically more abstract, more analytic way than before. And if Johnny Can’t Add with the new math, maybe Jenny Won’t Code with an overly abstract presentation of computing. Papert points us in the opposite direction: towards the origin of computing (or mathematics) being used to think about physics, science, economics … Harvey Mudd College increased the percentage of women in CS from 10% in 2006 to 48% in 2013, and this is what they did: bring fun to the first CS course, basing it on projects with relevant applications and giving students choices in the application topics; making it not scary by splitting students into sections with and without previous experience; and investing on the social and cultural context. Education, Papert says, is “much more related to love, than to logic.”
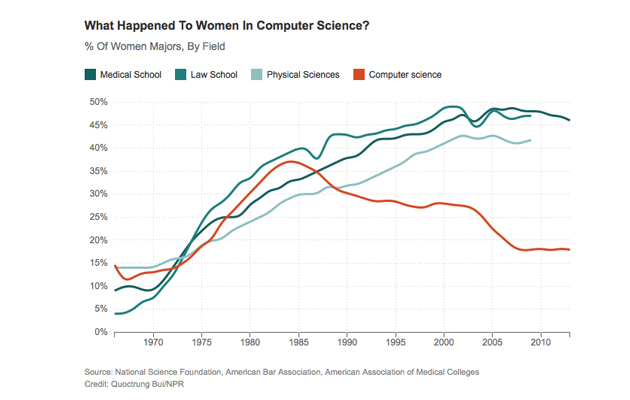
Percentage of degrees awarded to females, by field.
Another influential figure in this conversation is the computer science professor Mark Guzdial. His article “Education: Paving the Way for Computational Thinking,”4 emphasizes the theory of computation, not using computing to think about the world. With the phrase “understand computing” appearing a dozen times, it seems this article equates computational thinking with thinking about computing—which again is disempowering the idea. What’s interesting is that, in practice, Guzdial has worked tenaciously to introduce computing in a project-based, contextualized fashion with his Media Computation approach. In his TEDx talk on MediaComp, Guzdial does not use the word “abstraction” once; instead, his students “can use programs to understand their world, to manipulate their world."
Grady Booch, IBM Fellow and Chief Scientist of Watson/M, poked the idea of computational thinking in the right direction in his ACM Learning Webinar (Feb. 3). He noted that humans have outsourced part of our brain to our devices, changing the way we go about the world. There is incredible expressiveness in our algorithms, Booch says. His words hint at computing as a representation: “the technology of literacies”5. But he is still attached to Wing’s language, reducing the idea back to the components of abstraction, data, and algorithms.
Abstraction is not the badge of computer science: it’s integral to mathematics, philosophy, and all of science! And why fixate on decomposition, patterns and algorithms, and say nothing about variables and debugging? Naming things is essential to computing, and the idea of objects endowed with certain inherent properties is computationally powerful. There are many ways to draw on computing as a representation of knowledge, to help us think.
The operational aspect of making problems computable is essential, but not aspirational. Most people don't want to be a computer scientist, but everyone can use computers as an extension of our minds, to experience the world and create things that matter to us.
Computational thinking is epitomized by the Jupyter (IPython) Notebook delineating the analysis behind one of the biggest scientific discoveries of our time: the detection of gravitational waves by the LIGO collaboration. It can help us analyze the bike-sharing program in Paris, or explain how high humans can jump. It’s a source of power to do something and figure things out, in a dance between the computer and our thoughts. The inversion, starting with computing as a formal thing to understand and then come to the application later, takes away its power.
Notes / readings
1 Jeannette Wing (2006), Computational Thinking, Communications of the ACM, Vol. 49(3):33–35, http://dx.doi.org/10.1145/1118178.1118215
2 Seymour Papert, Mindstorms: children, computers, and powerful ideas, Basic Books, Inc. New York, NY; 1980. ISBN:0-465-04627-4 http://dl.acm.org/citation.cfm?id=1095592
3 Seymour Papert (1996), An Exploration in the Space of Mathematics Educations, International Journal of Computers for Mathematical Learning, Vol. 1, No. 1, pp. 95-123.
4 Mark Guzdial (2008), Education: Paving the way for computational thinking, Communications of the ACM 51, 8 (August 2008), 25-27. http://dx.doi.org/10.1145/1378704.1378713
5 Andrea diSessa (2008), Can students re-invent fundamental scientific principles? Evaluating the promise of new-media literacies, in T. Willoughby and E. Wood (ends.), Children’s learning in a digital world (pp. 218–248); Blackwell Publishing, Oxford, UK.
Special thanks
Much thanks to Chuck Severance and Idit Harel, who read a draft of this post and gave suggestions. Chuck gave me the idea of mentioning the drop in female participation in computer science.