Student guest blog post: pterosaur weight estimation
The second in a series of blog posts by the students of "Bio-aerial Locomotion" at GW, and part of a collaborative and interactive study of some controversial issues about giant pterosaurs' ability to fly.
The first student guest blog post (by Akash Druv and Alex Golding) addresses the quadrupedal-launch thesis of Prof. Michael Habib (and colleagues) about how pterosaurs took off from the ground. Although it has detractors, it appears that the quad-launch thesis is accepted by the community of pterosaur scientists. A subject that has caused even more debate in the field is the estimation of weight for these extinct creatures.
Weight Estimations for Q. Northropi & Other Pterosaurs
By Samantha Rogers & Eric Master
Pterosaurs (meaning "winged lizard") were flying reptiles which existed from the late Triassic to the end of the Cretaceous period. They are the earliest vertebrates known to have evolved powered flight. Their wings were made up of a membrane, skin and tissue, stretching from their ankles to their fingers. Pterosaurs spanned a wide range of adult sizes, from the smallest Nemicolopterus to the largest known flying creatures of all time, Quetzalcoatlus northropi.
Q. northropi had an estimated wingspan of 10-11 m. Due to this vast size and no living specimen, the mass estimates span a wide range. The National History Museum and Henderson (2009) predicted a mass of around 500 kg, whereas Witton more recently suggests a mass of around 250 kg. Yet another mass estimate, from Chatterjee and Templin (2004) placed the giant pterosaur at a wimpy 70 kg. Which one is more likely to be correct?
Weight estimations for pterosaurs with incomplete skeletons are quite confusing for non-paleontologists. There is no commonly accepted best way to calculate the weight of an incomplete skeleton. This leads to many competing methodologies, each with its own assumptions and flaws, and therefore many debates on the correct mass of a pterosaur. Even fully accepted parts of the field can seem so bizarre to outsiders that they are too easily dismissed as improbable.
The skeleton of pterosaurs
How can a creature with a wing span nearly the size of a school bus possibly be in the same weight range as a pony? Fossil records show that the bones of pterosaurs were hollow, similar to birds. These fossils also help us to understand the thickness of the bones. There are fossils with bone thickness as low as 10 mm. Considering the weight of the skeleton with this in mind, estimates of 200-250kg seem reasonable, despite the large size of Q. northropi.

University of Portsmouth hollow pterosaur wing bone.
The bones have a cross section of a nearly perfect ellipse that increases in size as the pterosaur does. The Relative Failure Force (RFF) of pterosaur bones is 1.9 times the RFF expected of a similarly sized bird. Despite the pterosaur bone layer only being 10-mm thick, it takes twice the force to break its wings as it would for a bird. This makes a pterosaur skeleton not only incredibly lightweight, but also more than up to the task of supporting the wing loading of such a large creature.
Pterosaur wings
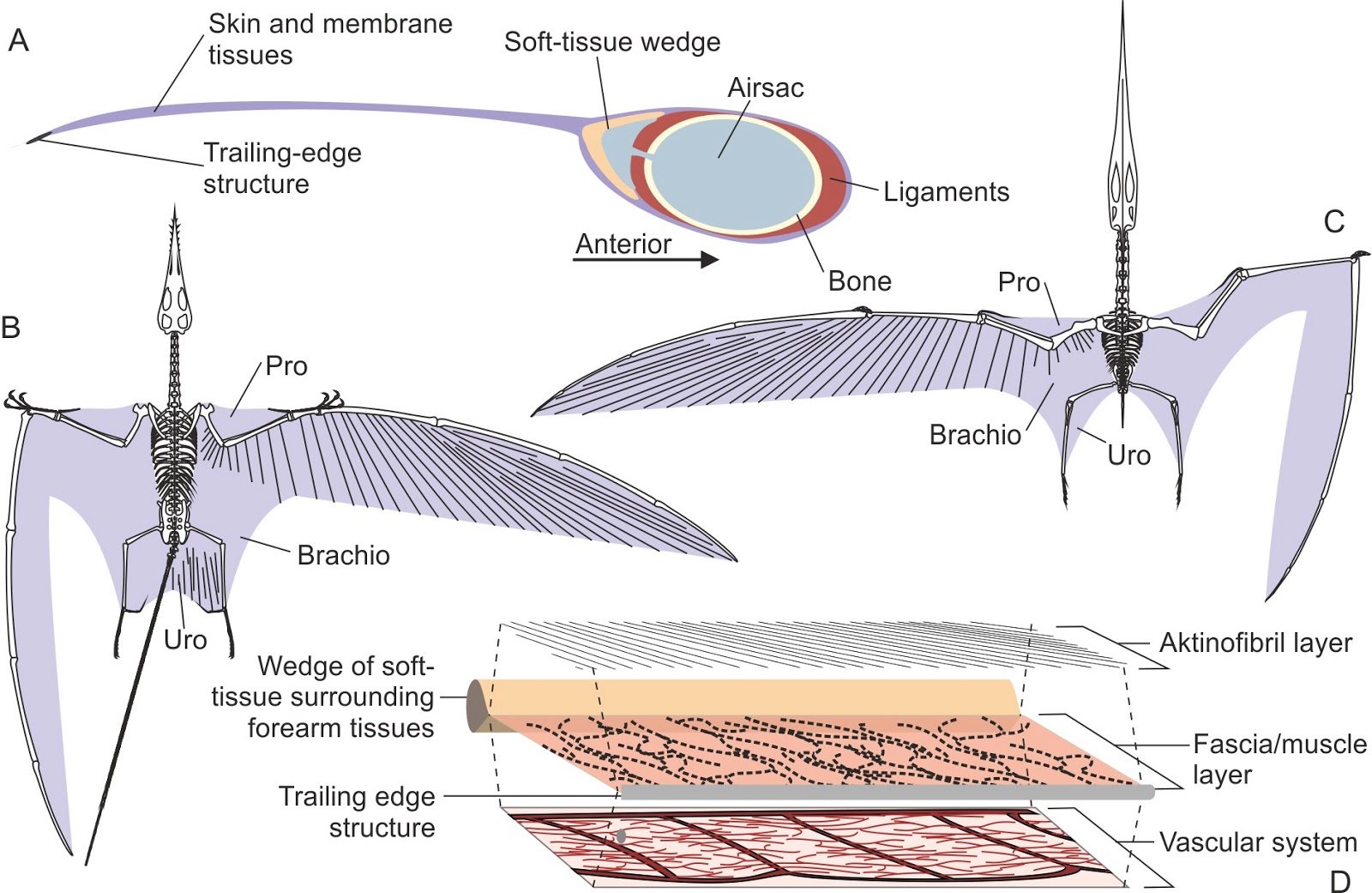
Analysis of pterosaur wing membranes by Mark Witton. Illustration from his recent book "Pterosaurs: Natural History, Evolution, Anatomy" (2013)
The flight membrane of a pterosaur is also constructed for lightweight strength. Unlike flimsy bat membranes, radiating out from a pterosaur’s arms are small stiff keratin rods called actinofilbrils. These fibers are .05 mm in diameter and are evenly spaced 0.2 mm apart throughout the membrane. Actinofilbrils run perpendicular to the arms and hands then slowly shift until they are nearly parallel to the fingers. This prevents the pterosaur wings from billowing and flapping while still being very lightweight, allowing pterosaurs to reach sizes well above those possible for bats.
Methods for weight estimation
With their understanding of pterosaur biology, paleontologists can estimate the weight of a pterosaur from its full skeleton quite accurately, but things are much harder when the scientists only have partial skeletons to work from. There are several different methods used for estimating the weight of a pterosaur from partial remains.
Using pterosaurs where both the body dimensions and probable mass are already known, a regression analysis can be developed using a specific known dimension (for example, body length) and mass. For unknown pterosaurs close in size to many known pterosaurs, this methodology can be accurate enough. If the pterosaur is much larger than any fully known pterosaur, like in the case of Q. northropi, the results of such an analysis can be highly inaccurate, up to three times larger than even the largest estimate.
Another methodology is to select a single fully known pterosaur that is closely related to the unknown pterosaur and simply scale up the fully known one. The results of this method are inaccurate but they do lie in the range of the correct mass, making it a good simple way to check if more complicated methods are yielding probable results. This method will not work if the fully known pterosaur is not closely related to the unknown one.
In a mathematical methodology called slicing, a model of the unknown pterosaur is sliced up into chunks. Each chunk is assigned its own density based upon observations of density in other pterosaurs and similar animals. The mass is then calculated from the volume multiplied by the density. Proven to be accurate in predicting the mass of different species of birds, it is nevertheless contingent upon having an accurate model of the pterosaur. Overestimating the length of the pterosaur, for example, can result in as much as a doubling of the mass.
How heavy was Quetzalcoatlus northropi?
One important thing to note is that all these methodologies require accurate models of the shape and size of the unknown pterosaur. In the real world, such estimations are sometimes very hard to come by. In 2009, Donald Henderson attempted to model Q. northropi using the mathematical slicing methodology. Instead of making his own estimations of body type and size, Henderson used estimations made by Wellnhofer and Langston, predicting a wingspan of 11.2 m and a torso length of 1.8 m. His result was a weight of 544 kg —much too heavy for Q. northropi to have possessed the capability of active flight.
The next year, Witton & Habib published a paper on the ability of Q. northropi to fly. According to them, a much better estimate for torso length would be .67 m, which would have reduced its weight to 240 kg. Unfortunately for both Henderson and any untrained observers, Witton & Habib based this new estimates on unpublished data by Habib and personal communications with Langston. Witton & Habib provide no data or explanation on why the new estimate of torso length is better than the old one, except to say that it is consistent with the proportions of the smaller specimens called Quetzalcoaltus sp.
Summary notes from two recent papers on pterosaur weight
Henderson, 2009:
He estimates a weight of 544 kg, which would make Q. northropi incapable of flight. The weight of the Q. northropi model can be reduced to 198 kg, but the resulting model neither has the internal space for the lungs and other organs, nor sufficient musculature to enable takeoff and active flight. The body width and depth is reduced by 20% and 25% respectively from the model used for the rest of the calculations.
There is a notable gap between the weight of Q. northropi and the other "giant" pterosaurs, like Tupuxuara. Tupuxuara weighs in at 22.8 kg, nearly half the weight of the largest flying modern birds at 41 kg. This gap mirrors the gap between the weights of modern flightless birds and their flying counterparts. It is also of note that it took approximately 80 million years for birds to go from flying to flightless, while the Q. northropi would have had 160 million years to develop flightlessness.
Witton & Habib, 2010:
Henderson’s models failed because he used a body length estimate of 1.8 meters when he should have used an estimate of 0.65 meters. The new estimation of body length is based upon unpublished data and no attempts are made to justify if the new internal space is enough to house the biological necessities, as brought up by Henderson. (There is mention on Wikipedia of some pterosaurs having their special lungs actually extending out onto their wing. This would free up space in their main body making this model more probable.)
Wing span is extremely important—a pterosaur with a 13-m wingspan would have twice the mass of a pterosaur with a 10-meter wingspan. Witton & Habib suggest that overestimation of wingspan is in large part responsible for what he considers an overestimation of weight.
Q. northropi is a member of the Azhdarchid family of pterosaurs. While Tupuxuara is closely related to the Azhdarchid family, there are key differences in the head and neck area that would cause an overestimation of weight it it were scaled to Q. northropi size.
Of note in the argument about using birds to make predictions for pterosaurs—bird bones grow more slender as the bird increases in size, so that bird wings would snap after a certain span, limiting their flying size. Pterosaurs show the opposite: their bones increase in diameter as they grow larger, which allows them to have much larger wingspans without fear of damage.
References:
- "Hollow Pterosaur Wing-bone." Palaeobiology. University of Portsmouth, n.d. Web. 25 Nov. 2013.
- Chatterjee, Sankar and Templin R.J. “Posture, Locomotion, and Paleoecology of Pterosaurs” Colorado: The Geological Society of America, Inc., 2004. // Read in Google Books
- Henderson, Donald M. “Pterosaur body mass estimates from three-dimensional mathematical slicing,” Journal of Vertebrate Paleontology, Vol. 30(3):768–785 (2010), doi:10.1080/02724631003758334
- Witton, Mark P., David M. Martill and Robert F. Loveridge, "Clipping the wings of giant pterosaurs: Comments on wingspan estimations and diversity," Acta Geoscientica Sinica, Vol. 31:79–81 (2010). // find at markwitton.com
- Witton, Mark P. and Michael B. Habib, “On the size and flight diversity of giant pterosaurs, the use of birds as pterosaur analogues and domments on pterosaur flightlessness,” PLOS One (2010), doi:10.1371/journal.pone.0013982
- Witton, Mark P. "Quetzalcoatlus Northropi (again)." Flickr. Yahoo!, 17 Nov. 2006. Web. 25 Nov. 2013.
- Witton, Mark P. Pterosaurs. Natural History, Evolution, Anatomy. Princeton: Princeton Univ. Press, 2013.
The "reverse mass estimation" method
by Robert Forcha
In the context of the much-debated estimates of weight for Quetzalcoatlus northropi, a different approach was attempted by Jim Cunningham, who estimated the mass of Quetzalcoatlus using a “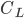 -tuning method.” Following this procedure, a mass estimate was generated “in reverse” from aerodynamic formulae. This can be done by using the standard lift equation:
-tuning method.” Following this procedure, a mass estimate was generated “in reverse” from aerodynamic formulae. This can be done by using the standard lift equation:
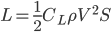
where 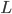 is the lift force,
is the lift force, 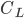 is the lift coefficient,
is the lift coefficient, 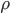 is the air density,
is the air density, 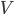 the flight speed and
the flight speed and 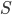 the wing surface area.
the wing surface area.
Assuming an air density of 1.25 kg/m3, a lift coefficient of 0.6 (standard for birds), and a modeled wing surface area of 11.36 m2, the lift force and cruising speed are the only remaining variables. In order to estimate the weight, the concept of wing loading, a ratio of weight to wing surface area, is utilized. According to the Great Flight Diagram (Tennekes, 2009), other pterosaurs of comparable size would require a wing loading of approximately 220 kg/m2. This yields a weight of about 2500 N. Dividing this weight by the acceleration of gravity yields an approximate mass of 250 kg. From here, the cruising speed can also be estimated.
According to Witton and Habib (2010), these estimates are in line with those of Paul Henderson (using an updated model). Use of this method brings up a few issues with regard to validity, such as assuming flight, making assumptions about the anatomy of an extinct species very little is known about, and the effect of other assumptions made during the calculations.
One of the primary issues with this method is the assumption of flight. Much of the debate taking place over this very large pterosaur is whether or not it was flight-capable. Low-mass simulations have failed, while “heavier” models have offered successful simulations. Due to the number of unknowns in all of these analyses, the importance of mass in the calculations cannot be completely determined. In any case, taking the position from the start that Q.n. was capable of flight seems like bad practice in trying to determine an unknown mass, which will contribute to the argument of whether or not Q.n. was capable of flight! Fortunately, the results with this method are in agreement with those calculated from the fossils and using “slicing methods.”
Another issue is the level of assumption made about the anatomy of Q.n. One would assume that in the 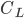 tuning method, much about the wing and body anatomy of the subject would need to be known. Due to the poor condition of the known Q.n. fossil, this is not the case. Many of these fossils are laterally crushed, so many assumptions have been made about the transverse dimensions of the pterosaur. According to Witton (2008):
tuning method, much about the wing and body anatomy of the subject would need to be known. Due to the poor condition of the known Q.n. fossil, this is not the case. Many of these fossils are laterally crushed, so many assumptions have been made about the transverse dimensions of the pterosaur. According to Witton (2008):
“Pterosaur anatomy is too poorly understood to back-calculate mass from results of aerodynamic calculations: it is currently difficult to distinguish the effects of greater masses on failed pterosaur flight models from incorrect assumptions of wing shape, flight energetics or takeoff mechanics.”
Also, it has been noted that basing all anatomy assumptions on the anatomies of modern birds can be misleading, as pterosaurs seem to be a very unique family of species. Finally, the assumptions made during calculations could have a significant effect on their outcome. Anatomical assumptions, such as wing shape, wing span, skeletal density, and overall average density must be made (or obtained from ever-changing models). In the estimates made by Henderson (2010), different densities were used for different parts of the body, and all were based on (reasonable) assumptions. The wide range of possibilities in these assumptions make this a very tricky path to navigate. It seems all methods of mass estimation have this problem, though, as is demonstrated by the fairly large standard deviations in all of the papers we have read on the subject.
In conclusion, Mr. Cunningham’s method does seem to provide results that agree with the prevailing mass estimates for Q.n. However, due to the number of assumptions made, this method is best used as validation for models and estimates created from fossils, and should not be used as “evidence” for flight ability. However, as this method is developed further, it should make an excellent tool for checking results when estimating mass for extinct avian species.
References
- Hank Tennekes. The Simple Science of Flight, Second Edition, MIT Press, 2009.
- Mark Witton, Michael Habib. "On the size and flight diversity of giant pterosaurs, the use of birds as pterosaur analogues and comments on pterosaur flightlessness," PLOS One (2010), doi:10.1371/journal.pone.0013982)
- Mark Witton. "A new approach to determining pterosaur body mass and its implications for pterosaur flight," Zitteliana B28, 2008 // PDF from markwitton.com
- D. M. Henderson. "Pterosaur body mass estimates from three-dimensional mathematical slicing," Journal of Vertebrate Paleontology, Vol. 30(3):768–785 (2010) doi:10.1080/02724631003758334
