Student guest blog post: the Wagner effect

The starting vortex at the trailing edge, as visualized by Prandtl in 1934 using a water channel and aluminum particles.
The fourth and final student guest post explains the Wagner effect, and its role in animal flight. We hope you enjoy the series of posts from GW students of animal locomotion!
The previous guest posts are:
This post completes the series, which was inspired by the entertaining cross-comment thread to a Google+ post of Michael Habib (Sept.22, 2013).
The Wagner effect
by Olivier Mesnard, Prithviraj Pawar, Liangwei (Starson) Li
Both experiments and numerical simulations have shown that the aerodynamic forces acting on a wing accelerating from rest are lower than the values predicted by quasi-steady models (which assume steady-state forces are produced at each instant in time). A transition period is needed before the forces reach the steady-state value. This latency in the establishment of lift was first proposed by Wagner (1925) and studied experimentally by Walker (1931).
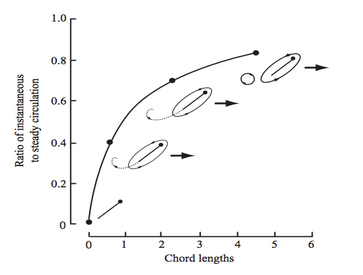
Wagner effect: growth of the circulation to a steady-state due to the shedding of the starting vortex (from Sane, 2003).
The Wagner effect can be described in terms of circulation around an airfoil: as a wing starts impulsively from rest, the circulation around it does not immediately attain its steady-state value. Thus, when any wing first starts moving through the air, it must travel several chord-lengths before reaching the steady-state circulation around it (Dickinson & Götz, 1993 & Sane, 2003; see figure, left).
The Wagner effect is the consequence of two phenomena. First, when the wing is accelerating from rest, vorticity is generated around it (called the bound vortex) and shed at the trailing edge, where it rolls up forming the starting vortex (see feature image, above). This trailing-edge vortex can be observed on insect wings, but also on the wings of a commercial jetliner. The starting vortex induces a velocity field that counteracts that of the circulation bound to the wing. The influence of the starting vortex on the airfoil decreases as it is convected away from the trailing edge by the free-stream velocity.
Second, the fluid viscosity slows the development of the bound vortex, so we could conclude that the delay in reaching steady state will be amplified at low Reynolds numbers. However, the experiments of Dickinson & Götz (1993) with model insect wings showed that the delay in build-up of lift is less noticeable at lower Reynolds numbers, in the range 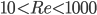 . (The experiments of Walker used
. (The experiments of Walker used 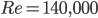 .) It appears that the dependence of the Wagner effect on Reynolds number is not firmly established.
.) It appears that the dependence of the Wagner effect on Reynolds number is not firmly established.
Wagner's function
When designing either an aircraft or a bio-inspired robot, engineers have to explore many design alternatives to optimize performances of the device. This can be very time-consuming. That is why usually only quasi-steady aerodynamic models are employed (which are fast and robust). But those models do not take into account the possible unsteady effects that can occur during rapid manoeuvres or takeoff, such as the Wagner effect.
Using linearized thin-airfoil theory for the impulsive motion of an airfoil in an incompressible flow, a relation can be derived for the unsteady lift generated, as a function of time (Fung, 2002, p. 207). The unsteady lift for an airfoil of chord 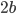 , impulsively started to velocity
, impulsively started to velocity 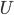 , has the following form:
, has the following form:
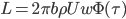
Here, 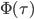 is called Wagner’s function (see a plot, below). It corrects the quasi-steady models when obtaining the aerodynamic forces during the transitional period. The angle of attack,
is called Wagner’s function (see a plot, below). It corrects the quasi-steady models when obtaining the aerodynamic forces during the transitional period. The angle of attack,  , is assumed small, and
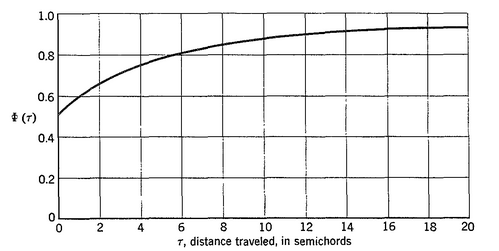
, is assumed small, and 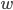 is the downwash velocity:
is the downwash velocity: 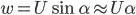 .
.
Wagner's function for an impulsively started airfoil in an incompressible fluid. The value of lift starts at 50% of the steady-state value. (Fung, 2002; p. 207)
Although Wagner's function can be derived analytically, good approximate expressions have been calculated (some of them can be found in Fung’s book).
The clap-and-fling mechanism
Some insects, as well as some birds, use mechanisms to quickly build the circulation around their wings during take-off, and therefore attenuate the Wagner effect. The clap-and-fling mechanism was first described by Weis-Fogh (1973) to explain how certain insects and birds are able to increase the amount of generated lift.
The mechanism starts before the pronation (rotational movement on the wing between the upstroke and the downstroke) with the apposition of the two wings. The wings are then rotated about the trailing edge. The void created by the separation of the leading edges is rapidly filled with air generating a circulation. It also produces counter-rotating vortices above the animal that give extra lift. Once the pronation is done, the downstroke begins.
The clap-and-fling mechanism is mostly used by insects; however, some birds have developed this function as well. For example, the pigeon uses this technique during lift-off (see photograph) producing a recognizable sound. But mostly, it is observed that the birds do not often use the clap-and-fling mechanism to overcome the Wagner effect (Sane, 2003). This suggests that the Wagner effect might not have much effect on bird flight. Some birds (e.g., pigeon) may be using a clap-and-fling motion just to obtain maximum amplitude by the wings, rather than to overcome the Wagner effect.
Photograph of a pigeon clapping its wings at the top of the upstroke, for take-off. Credit: Joe Hancuff, @joehancuff on Twitter.
Does the Wagner effect apply to pterosaur flight?
As previously stated, the latency to build circulation applies to any accelerating wings. According to Habib, the Wagner effect is an important factor for any animal flyer during launch and is often underestimated. Even if this delay is more significant at low Reynolds numbers, one could wonder if the Wagner effect affects a pterosaur to get off the ground?
There are two schools of thought about the take-off of the pterosaur: bipedal launch and quadrupedal launch. Witton and Habib (2010), some of the avid proponents of a quadrupedal launch, maintain that the bipedal launch position would have placed the wings in a stall configuration, a real problem to quickly build circulation. Habib (2008) mentioned that the pterosaur could reach steady-state lift faster by having high launch accelerations (more plausible with a quadrupedal launch, using the forelimbs and the hindlimbs) and opening the wing rapidly by flinging it outwards and forward during the ballistic phase, thereby overcoming the Wagner effect.
Alexander and Vogel (2004) suggest that the Wagner effect is magnified at low Reynolds numbers (where viscous effects dominate over inertial effects). However, some results contradict this statement. The experiments of Dickinson and Gotz (1993) at Re=10–103 show little evidence of Wagner’s effect. For the first one-chord-length of travel, the lift increases quickly, under the effect of a finite acceleration. Upon reaching uniform velocity, the lift dips sharply, then slightly increases for about one extra chord length of travel. The authors identify this last stage of lift increase as evidence of Wagner’s. But by 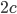 of travel, steady-state lift is established.
of travel, steady-state lift is established.
We were not able to find Walker’s paper (1931), but other sources say his experiments at Re=140,000 agree with Wagner’s prediction. Beckwith and Babinsky (2009) conducted some experiments on a flat plate at a Reynolds number about 60,000 that show the Wagner effect is negligible after about one chord length of travel. Considering that the Reynolds number is estimated to range from 104 to 106 for pterosaurs, it is reasonable to think that the latency would be negligible for pterosaurs. Therefore, using quasi-steady models could be adequate to evaluate aerodynamic forces acting on the pterosaur.
Moreover, it’s entirely plausible that the angle of attack during the first downstroke is in the post-stall region. In that case, other unsteady effects, such as delayed stall, will be more important than the Wagner effect.
References:
- Alexander D.E. and Vogel S. (2004). Nature’s flyers: birds, insects and the biomechanics of flight. JHU Press.
- Beckwith, R. M. H. and Babinsky, H. (2009). Impulsively started flat plate flow, Journal of Aircraft, Vol. 46(6):2186–2188.
- Dickinson M.H. and Gotz K.G. (1993). Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Exp. Biology, 174:45-64.
- Dickinson M.H., Lehmann F.O. and Sane S.P. (1999). Wing rotation and the aerodynamic basis of insect flight. Science, 284:1954-1960.
- Fung, Y. C. (2002). An introduction to the theory of aeroelasticity. Courier Dover Publications. // Read in Google Books
- Habib M.B. (2008). Comparative evidence for quadrupedal launch in pterosaurs. Wellnhofer Pterosaur Meeting: Zitteliana B28. Pp 161-168.
- Sane S.P. (2003). The aerodynamics of insect flight. J. Exp. Biology, 206:4191-4208.
- Walker, J. A. (2002). Rotational lift: something different or more of the same? Journal of Experimental Biology, 205(24), 3783-3792.
- Witton M.P. and Habib M.B. (2010). On the size and flight of the giant pterosaurs, the use of birds as pterosaur analogues and comments on pterosaur flightlessness. PLoS ONE 5(11).
- Walker, P. B.(1931). Growth of circulation about a wing and an apparatus for measuring fluid motion. Reports and Mem., Aeronaut. Res. Com. no. 1402.